Попеленский М.Ю.
Анализ управляемости. Декомпозиция по управлению. Стабилизация
Теория
Рассмотрим линейную стационарную управляемую систему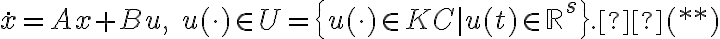
Здесь 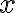 --
-- 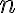 -мерный вектор-столбец координат, описывающий состояние управляемого объекта,
-мерный вектор-столбец координат, описывающий состояние управляемого объекта, 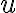 --
-- 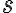 -мерный вектор-столбец управляющих воздействий,
-мерный вектор-столбец управляющих воздействий, 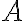 -- постоянная матрица размерности (
-- постоянная матрица размерности (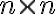 ),
), 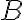 -- постоянная матрица размерности (
-- постоянная матрица размерности (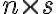 ),
), 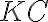 -- пространство векторных кусочно-непрерывных функций,
-- пространство векторных кусочно-непрерывных функций, 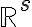 --
-- 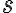 -мерное пространство позиционных управлений.
-мерное пространство позиционных управлений.
Определение. Система (**) называется полностью управляемой, если ее можно перевести из любого начального состояния в любое конечное с помощью управления 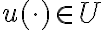 за конечное время.
за конечное время.
Определение. Матрица 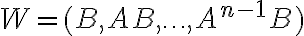 называется грамианом управляемости.
называется грамианом управляемости.
Теорема. Для полной управляемости системы (**) необходимо и достаточно, чтобы 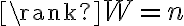 .
.
Следствие. При $s=1$ критерий управляемости принимает вид: 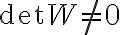 .
.
Примечание. Для того, чтобы система (**) при 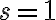 была представима в виде одномерной управляемой системы, необходимо и достаточно, чтобы система была полностью управляемой.
была представима в виде одномерной управляемой системы, необходимо и достаточно, чтобы система была полностью управляемой.
Теорема. (О декомпозиции) Если система (**) не является полностью управляемой, то она представима в виде двух подсистем,
одна из которых полностью управляема в своем подпространстве, а другая является неуправляемой.

Социальные сети