Попеленский М.Ю.
Анализ наблюдаемости. Декомпозиция по наблюдению
Теория
Рассмотрим линейную стационарную систему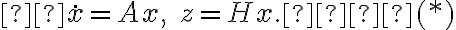
Здесь 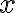 --
-- 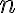 -мерный вектор-столбец координат, описывающий
-мерный вектор-столбец координат, описывающий
состояние системы, 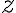 --
-- 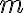 -мерный вектор-столбец измерений (в
-мерный вектор-столбец измерений (в
подавляющем большинстве случаев 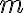 ),
), 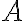 -- постоянная матрица
-- постоянная матрица
размерности (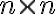 ),
), 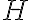 -- постоянная матрица размерности
-- постоянная матрица размерности
(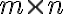 ).
).
Определение. Система (*) называется наблюдаемой в момент времени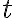 , если существует конечный момент времени
, если существует конечный момент времени 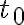 такой, что можно
такой, что можно
определить состояние системы $x(t)$ из наблюдения выходной функции
$z(\tau)$ на отрезке ![[t_0,t] [t_0,t]](https://copy.distant.msu.ru/filter/tex/pix.php/02fde54e2053813582fb5a3ae44294b8.png) .
.
Определение. Матрица\( H \\ HA \\ \ldots\\ HA^{n-1} \right\)" alt="N=\left\( H \\ HA \\ \ldots\\ HA^{n-1} \right\)" src="https://copy.distant.msu.ru/filter/tex/pix.php/4f13ec7d2edea14f84371326b0cd1c8b.png" />
называется грамианом наблюдаемости.
Теорема.
Для наблюдаемости системы (*) необходимо и достаточно,
чтобы 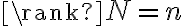 .
.
Следствие.
При 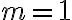 условие наблюдаемости принимает вид
условие наблюдаемости принимает вид 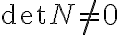 .
.
Определение.
Канонической формой Фробениуса по наблюдению называется следующая система: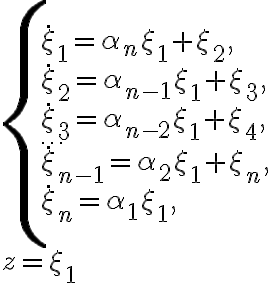
или в матричном виде: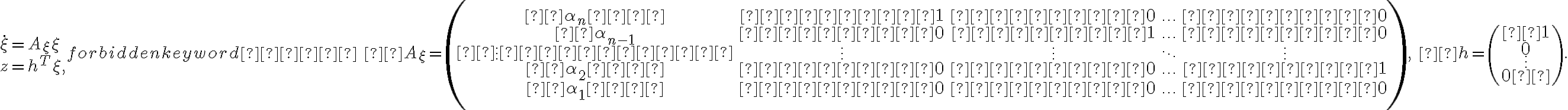
Теорема.
Система (*) наблюдаема тогда и только тогда, когда ее
можно записать в канонической форме Фробениуса по наблюдению.
Теорема.
(О декомпозиции) Если система (*) не является
полностью наблюдаемой, то она представима в виде двух подсистем,
одна из которых полностью наблюдаема в своем подпространстве, а
другая является ненаблюдаемой.

Социальные сети